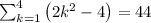Question

What is the sum of the series? 4 ∑k=1 (2k^2−4)

Answer 1

Hes right its 44

444444444444444444444

Answer 2

The sum of the series
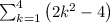`\sum_(k=1)^(4)\left(2 k^(2)-4\right)` is 44.

Explanation:

The given series is
`\sum_(k=1)^(4)\left(2 k^(2)-4\right)=44`

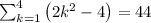
To find the sum of the series, we need to substitute the values for k in the series.

`\sum_(k=1)^(4)\left(2 k^(2)-4\right)=\left[2(1)^(2)-4\right]+\left[2(2)^(2)-4\right]+\left[2(3)^(2)-4\right]+\left[2(4)^(2)-4\right]`

Now, simplifying the square terms, we get,

`[2(1)-4]+[2(4)-4]+[2(9)-4]+[2(16)-4]`

Multiplying the terms,

`[2-4]+[8-4]+[18-4]+[32-4]`

Subtracting the values within the bracket term, we get,

`-2+4+14+28`

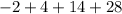
Now, adding all the terms, we get the sum of the series,

`\sum_(k=1)^(4)\left(2 k^(2)-4\right)=44`

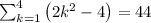
Thus, the sum of the series is
`\sum_(k=1)^(4)\left(2 k^(2)-4\right)=44`