Question

Which of the following describes the graph of y = x² - 225?

1) The graph has zeroes at x = 15 and x = 15 and it opens upward.
2) The graph has zeroes at x = -15 and x = -15 and it opens downward.
3) The graph has zeroes at x = 15 and x = -15 and it opens downward.
4) The graph has zeroes at x = 15 an x = -15 and it opens upward.

Answer 1

option 4. The graph has zeroes at x = 15 an x = -15 and it opens upward.

Explanation:

we have

`y=x^(2) -225`

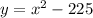
This is the equation of a vertical parabola open upward (the leading coefficient is positive)

The vertex represent a minimum

The vertex is the point (0,-225)

The axis of symmetry is x=0 (y-axis)

Find the x-intercepts (values of x when the value of y is equal to zero)

For y=0

`0=x^(2) -225\\x^2=225`

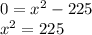
square root both sides

`x=\pm15`

therefore

The graph has zeroes at x = 15 an x = -15 and it opens upward.