Question

Line AB passes through point C(5,0) and is perpendicular to the line with the equation 3x-5y+17=0. determine the equation, in general form, for the line AB

Answer 1

The equation of line AB in general form is 5x + 3y - 25 = 0

Solution:

Given that we have to find the equation of line AB

The equation of line in slope intercept form is given as:

y = mx + c ------ eqn 1

Where, "m" is the slope of line and "c" is the y intercept

Given equation of line is:

3x - 5y + 17 = 0

Rearrange into slope intercept form

5y = 3x + 17

`y = (3x)/(5) + (17)/(5)`

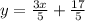
On comparing the above equation with eqn 1,

`m = (3)/(5)`

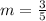
We know that,

Product of slope of line and slope of line perpendicular to given line is equal to -1

`(3)/(5) * \text{ slope of line perpendicular to given line } = -1\\\\\text{ slope of line perpendicular to given line } = (-5)/(3)`

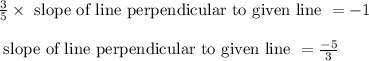
Now find the equation of line AB with slope
`(-5)/(3)` and passes through point C(5,0)

`\text{Substitute } m = (-3)/(5) \text{ and } (x, y) = (5, 0) \text{ in eqn 1}`

`0 = ((-5)/(3)) * 5 + c\\\\0 = (-25)/(3) + c\\\\0 = (-25+3c)/(3)\\\\-25+3c = 0\\\\3c = 25\\\\Divide\ both\ sides\ of\ equation\ by\ 3\\\\c = (25)/(3)`

`\text{Substitute } c = (25)/(3) \text{ and } m = (-5)/(3) \text{ in eqn 1 }\\\\y = (-5)/(3) * x + (25)/(3)\\\\y = (-5x)/(3)+(25)/(3)`

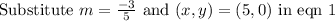
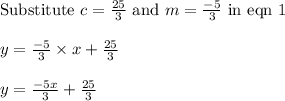
Let us write the equation in general form

The standard form of an equation is Ax + By = C

In this kind of equation, x and y are variables and A, B, and C are integers

`y = (-5x)/(3) + (25)/(3)\\\\3y = -5x + 25\\\\5x +3y -25 = 0`

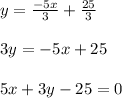
Thus equation of line AB in general form is 5x + 3y - 25 = 0