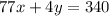Question

What is the equation of a line that passes though the points (0,85) and (4,8)?

Answer 1

The equation of line is:

`77x+4y=340`

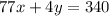
Explanation:

Given points:

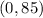`(0,85)` and
`(4,8)`

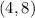
To find the equation of the line.

Solution:

In order to find the equation of the line we will first find the slope of the line.

The slope of a line passing through points
`(x_1,y_1)` and
`(x_2,y_2)` the slope can be given as:

`m=(y_2-y_1)/(x_2-x_1)`

Plugging in the given points to find the slope of the line.

`m=(8-85)/(4-0)`

`m=(-77)/(4)`

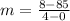
Equation of line can be written in point slope form as:

`y-y_1=m(x-x_1)`

where
`(x_1,y_1)` is a point on the line.

Using point (4,8)

`y-8=-(77)/(4)(x-4)`

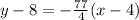
Multiplying both sides by 4.

`4(y-8)=4.(-(77)/(4))(x-4})`

`4(y-8)=-77(x-4)`

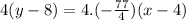
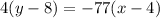
Using distribution:

`4y-32=-77x+308`

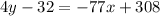
Subtracting
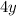`4y` both sides.

`4y-4y-32=-77x-4y+308`

`-32=-77x-4y+308`

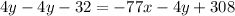
Subtracting 308 both sides.

`-32-308=-77x-4y+308-308`

`-340=-77x-4y`

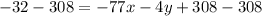
Multiplying each term with -1.

`340=77x+4y`

Thus, equation of line is:

`77x+4y=340`