Question

The table below shows all of the possible outcomes for rolling two six-sided number cubes. A table with 36 possible outcomes. There are 9 desired outcomes. What is the probability of rolling an even number first and an odd number second?

Answer 1

c) 1/4

Explanation:

Answer 2

The image is missing, we have attached the image.

Answer:

The of getting an even number in first and an odd number second is
`(1)/(4)\ or\ 0.25`.

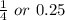Explanation:

Given,

Total number of outcomes = 36

We have to find the probability of rolling an even number first and an odd number second.

Solution,

Firstly we will find out the possible outcomes;

`(2,1),\ (2,3),\ (2,5),\ (4,1),\ (4,3),\ (4,5),\ (6,1),\ (6,3),\ (6,5),`

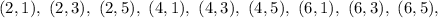
So the total number of outcomes = 9

Now according to the formula of probability, which is;

`P(E)=\frac{\textrm{total number of possible outcomes}}{\textrm{total number of outcomes}}`

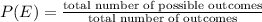
Now on putting the values, we get;

P(of getting an even number in first and an odd number second)=
`(9)/(36)=(1)/(4)=0.25`

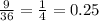
Hence The of getting an even number in first and an odd number second is
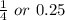`(1)/(4)\ or\ 0.25`.