Question

Graph ​ g(x)=3x2−12x−3 ​.

Answer 1

See the image.

Explanation:

The function is given by
`g(x) = 3x^(2) - 12x - 3`.

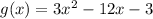Differentiating the function, we get
`(d g(x))/(dx) = 6x - 12`.

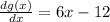Now, at x = 2, 6x - 12 will be 0.

Hence, at x = 2, either the function will have maximum or minimum value.

g(2) = 12 - 24 -3 = -15.

g(1) = 3 -12 -3 = -12.

g(0) = -3.

Hence, the given function passes through (2, -15), (1, -12) and (0, -3).