Question

If a rectangle has an area of 2x^2+7x+3 find the perimeter

Answer 1

Perimeter of the rectangle=6x+8 square units

Explanation:

Given that area of rectangle is
`2x^2+7x+3`

Area of rectangle=lw square units

`2x^2+7x+3=2x^2+x+6x+3`

`=x(2x+1)+3(2x+1)`

`=(x+3)(2x+1)`

`2x^2+7x+3=(x+3)(2x+1)`

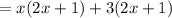
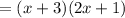
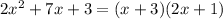
Comparing the above equation with the given area we get

lw=(x+3)(2x+1)

Therefore length=x+3 and width=2x+1

To find the perimeter :

Perimeter of the rectangle=2(l+w) square units

`=2((x+3)+(2x+1))`

`=2(x+3+2x+1)`

`=2(3x+4)`

`=6x+8`

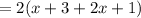
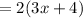
Therefore perimeter of the rectangle=6x+8 square units