Question

If a rectangle has an area of 2x^2+7x+3 find the perimeter

Answer 1

Perimeter of a rectangle = 6x + 8

Solution:

Given area of a rectangle =
`2x^2+7x+3`

Let us first factor the given polynomial.

`2x^2+7x+3=2x^2+x+6x+3`

`=(2x^2+x)+(6x+3)`

Taking out common terms in the above expression

`=x(2x+1)+3(2x+1)`

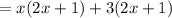
Taking out common term
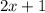`2x+1` in the above expression

`=(2x+1)(x+3)`

`2x^2+7x+3=(2x+1)(x+3)`

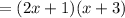
Area of a rectangle = l × b

Therefore,
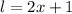`l=2x+1` and
`b=x+3`

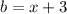
Perimeter of a rectangle = 2(l + b)

`=2[(2x+1)+(x+3)]`

`=2(2x+1+x+3)`

`=2(3x+4)`

`=6x+8`

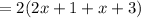
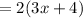
The answer is same if you take l = x + 3 and b = 2x + 1.

Hence, perimeter of a rectangle = 6x + 8.