Question

Suppose C and D represent two different school populations where C > D and C and D must be greater than 0. Whitch of the following expressions is the largest? Explain why. A. (C+D)^2 B. 2(C+D) C. C^2 + D^2 D. C^2 - D^2

Answer 1

A. (C+D)^2 is the largest expression

Explanation:

Squaring Properties

The square of a number N is shown as N^2 and is the product of N by itself, i.e.

`N^2=N*N`

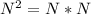
If N is positive and less than one, its square is less than N, i.e.

`N^2<N, \ for\ 0<N<1`

If N is greater than one, its square is greater than N

`N^2>N, \ for\ N>1`

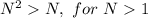
We have the following information: C and D represent two different school populations, C > D, and C and D must be positive. We can safely assume C and D are also greater or equal than 1. Let's evaluate the following expressions to find out which is the largest

A. (C+D)^2

Expanding

`(C+D)^2=C^2+2CD+D^2`

Is the sum of three positive quantities. This is the largest of all as we'll prove later

B. 2(C+D)

The extreme case is when C=2 and D=1 (recall C>D). It results:

2(C+D)=2(3)=6

The first expression will be

(3)^2=9

Any other combination of C and D will result smaller than the first option

C.
`C^2 + D^2`

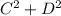
By comparing this with the first option, we see there are two equal terms, but A. has one additional term 2CD that makes it greater than C.

D.
`C^2 - D^2`

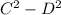
The expression can be written as

(C+D)(C-D)

Comparing with A.

`(C+D)^2=(C+D)(C+D)`

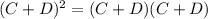
The subtracting factor (C-D) makes this product smaller than A which has two adding factors.

Thus A. is the largest expression