Answer:
a)
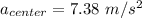
b)
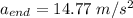
c)
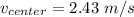
Step-by-step explanation:
a) Immediately after the rod is released, the rod is still horizontal but now subject to gravity. Since one end of the rod is fixed, then the weight of the rod applies a torque. Then by Newton's Second Law, the acceleration can be found.
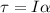
where I is the moment of inertia of the rod with respect to its fixed end, and α is the angular acceleration.
The net torque of the rod is
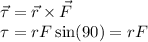
where r is the distance from center of the mass to the fixed end, so r = 0.4 m.
The weight of the rod is w = mg = 0.26 x 9.8 = 2.54 N.
So the net torque is τ = 1.01 Nm.
The moment of inertia of the rod is
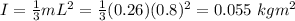
So, the Newton's Second Law yields
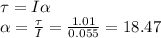
The relation between angular acceleration and linear acceleration is a = αr
So, the linear acceleration of the rod is
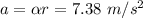
b) Using the same relationship between angular acceleration and linear acceleration, the linear acceleration of the end of the rod can be found.
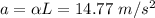
c) The conservation of energy can be used to find the velocity when the rod is vertical.
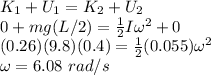
The linear velocity is v = ωr, so
v = 2.43 m/s.