Question

A new car is purchased for 24000 dollars. The value of the car depreciates at 6.75% per year. To the nearest year, how long will it be until the value of the car is 15500 dollars?

Answer 1

To the nearest year, it will take about 6 years for the value of the car to reach $15,500.

Step-by-step explanation:

To find how long it will take for the value of a car to depreciate to $15,500, we can set up an equation using the formula for exponential decay: V = P
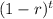`(1 - r)^t`, where V is the final value, P is the initial value, r is the depreciation rate, and t is the time in years.

Plugging in the given values, we have 15500 = 24000
`(1 - 0.0675)^t`. To solve for t, we can take the logarithm of both sides:

log(15500) = log(24000
`(1 - 0.0675)^t)`

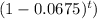
t * log(1 - 0.0675) = log(15500/24000)

t = log(15500/24000) / log(1 - 0.0675)

Using a calculator, we find that t is approximately 5.54 years. Rounding to the nearest year, it will take about 6 years for the value of the car to reach $15,500.