Answer:
0.71%
Explanation:
Given that a normally distributed set of data has a mean of 102 and a standard deviation of 20.
Let X be the random variable
Then X is N(102, 20)
We can convert this into standard Z score by
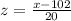
We are to find the probability and after wards percentage of scores in the data set expected to be below a score of 151.
First let us find out probability using std normal table
P(X<151) =
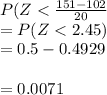
We can convert this into percent as muliplying by 100
percent of scores in the data set expected to be below a score of 151.
=0.71%