Answer:
v = <2, 2√3>
Explanation:
Let v be the vector of form <x,y>
Since its determinant is |4|, then:
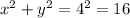
If it makes a π/3 angle with the positive x-axis, then the tangent relationship yields:
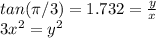
Replacing in the first equation:
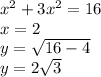
Therefore, v can be represented in component form as v = <2, 2√3>.