Answer:
1.505
Step-by-step explanation:
cylindrical part of diameter d is loaded by an axial force P. This causes a stress of P/A, where A = πd2/4. If the load is known with an uncertainty of ±11 percent, the diameter is known within ±4 percent (tolerances), and the stress that causes failure (strength) is known within ±20 percent, determine the minimum design factor that will guarantee that the part will not fail.
stress is force per unit area
stress=P/A
A = πd^2/4.
uncertainty of axial force P= +/-.11
s=+/-.20, strength
d=+/-.04 diameter
fail load/max allowed
minimum design=fail load/max allowed
minimum design =s/(P/A)
sA/P
A=(
 .96d^2)/4, so Amin=
.96d^2)/4, so Amin=
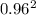 (because the diameter at minimum is (1-0.04=0.96)
(because the diameter at minimum is (1-0.04=0.96)
minimum design=Pmax/(sminxAmin)
1.11/(.80*.96^2)=
1.505