Answer:
The values are
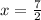 and
and
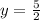
The solution is (
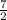 ,
,
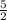 )
)
Explanation:
Given equations are
 and
and

To solve the given equations by elimination method:
Equation (1) can be written as
 and
and
Now multiply the equation (2) into 5 we get

Subtracting equations (3) and (4) we get
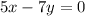
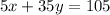
_________________
-42y=-105

Therefore
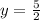
Substitute the value
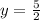 in equation (1) we get
in equation (1) we get
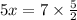
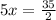
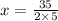
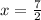
Therefore
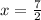 and
and
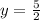
The solution is (
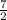 ,
,
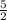 )
)