Question

A government watchdog association claims that 70% of people in the U.S. agree that the government is inefficient and wasteful. You work for a government agency and asked to test this claim to determine if the true proportion differs from 70%. You find that in a random sample of 1165 people in the U.S., 746 agreed with this view. Test the claim at 0.02 level of significance and determine which one of the following is a correct conclusion?

A.There is not sufficient evidence that the true population proportion is not equal to 70%.
B.There is sufficient evidence that the true population proportion is greater than 70%.
C.There is sufficient evidence that the true population proportion is less than 70%.
D.There is sufficient evidence that the true population proportion is not equal to 70%.

Answer 1

Option D) There is sufficient evidence that the true population proportion is not equal to 70%.

Explanation:

We are given the following in the question:

Sample size, n = 1165

p = 70% = 0.7

Alpha, α = 0.02

Number of people who agreed , x = 746

First, we design the null and the alternate hypothesis

`H_(0): p = 0.7\\H_A: p \\eq 0.7`

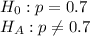
This is a two-tailed test.

Formula:

`\hat{p} = (x)/(n) = (746)/(1165) = 0.64`

`z = \frac{\hat{p}-p}{\sqrt{(p(1-p))/(n)}}`

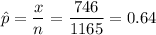
Putting the values, we get,

`z = \displaystyle\frac{0.64-0.7}{\sqrt{(0.7(1-0.7))/(1165)}} = -4.46`

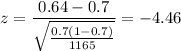
Now,
`z_(critical) \text{ at 0.02 level of significance } = \pm 2.33`

Since,

Since, the calculated z statistic does not lie in the acceptance region, we fail to accept the null hypothesis and reject it. We accept the alternate hypothesis.

Thus, there is enough evidence to support the claim that the true proportion differs from 70%.

Option D) There is sufficient evidence that the true population proportion is not equal to 70%.