Question

Use the laws of propositional logic to prove that each statement is a tautology. (p n q) rightarrow (p V r) p rightarrow (r rightarrow p) (8 points each for a total of 16, zyBook section 1.5, exercise 1.5.3(a, b))

Answer 1

See explanation below.

Step-by-step explanation:

If the statement is a tautology is true for all the possible combinations

Part a

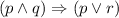`(p \land q) \Rightarrow (p \lor r)` lets call this condition (1)

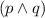`(p \land q)` condition (2) and
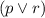`(p \lor r)` condition (3)

We can create a table like this one:

p q r (2) (3) (1)

T T T T T T

T T F T T T

T F T F T T

T F F F T T

F T T F T T

F T F F F T

F F T F T T

F F F F F T

So as we can see we have a tautology.

Part b

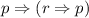`p \Rightarrow (r \Rightarrow p)` lt's call this condition 1

And
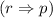`(r \Rightarrow p)` condition 2

We can create the following table:

p r (2) (1)

T T T T

T F T T

F T F T

F F T T

So is also a tautology.