Question

Prove the following statemnet: any natural number greater than 1 is divisible by a prime number

Answer 1

See the proof below

Explanation:

Proof

We can proof this using the well ordering principle.

Let's assume that k is a prime number >1. If k is a prime by definition is divisible by the prime number k.

Let's assume now that k is composite with the following form
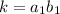`k = a_1 b_1` where
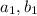`a_1, b_1` represent integers less than the number k.

Assuming that
`a_1` is prime then we have that
`a_1 | k` and we satisfy the conditions.

Now let's assume that
`a_1` is also composite with the following form
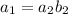`a_1 = a_2 b_2` as the product of two integers and for
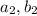`a_2, b_2` we assume that both are integers >1 and smaller than
`a_1`

If we continue this process t times dividing the composite factors into products of smaller factors we satisfy the condition that the set {
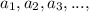`a_1, a_2, a_3,...,`} would be non empty.

And using the Well ordering principle we have t elements. From this we can conclude that
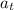`a_t` is prime and if we discompose this number we satisfy the existance of
`a_(t+1)` less than
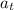`a_t` because we have this:

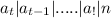`a_t |a_(t-1)|..... |a_!|n` with k a divisible prime.

And with this we satisfy the conditions and then the proof is complete.