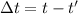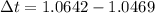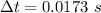Question

A trick shot archer shoots an arrow with a velocity of 30.0 m/s at an angle of 20.0 degrees with respect to the horizontal. An assistant standing on the level ground 30.0 m downrange from the launch point throws an apple straight up with the minimum initial speed necessary to meet the path of the arrow. What is the initial speed of the apple and at what time after the arrow is launched should the apple be thrown so that the arrow hits the apple?

Answer 1

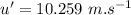`u'=10.259\ m.s^(-1)` is the initial velocity of tossing the apple.

the apple should be tossed after
`\Delta t=0.0173\ s`

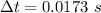
Step-by-step explanation:

Given:

• velocity of arrow in projectile,
  `v=30\ m.s^(-1)`

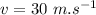
• angle of projectile from the horizontal,
  `\theta=20^(\circ)`

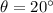
• distance of the point of tossing up of an apple,
  `d=30\ m`

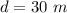
Now the horizontal component of velocity:

`v_x=v\ cos\ \theta`

`v_x=30* cos\ 20^(\circ)`

`v_x=28.191\ m.s^(-1)`

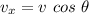
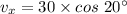
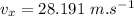
The vertical component of the velocity:

`v_y=v.sin\ \theta`

`v_y=30* sin\ 20^(\circ)`

`v_y=10.261\ m.s^(-1)`

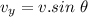
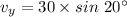
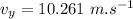
Time taken by the projectile to travel the distance of 30 m:

`t=(d)/(v_x)`

`t=(30)/(28.191)`

`t=1.0642\ s`

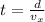
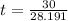
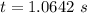
Vertical position of the projectile at this time:

`h=v_y.t-(1)/(2)g.t^2`

`h=10.261* 1.0642-(1)/(2) * 9.8* 1.0642^2`

`h=5.3701\ m`

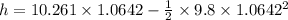
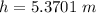
Now this height should be the maximum height of the tossed apple where its velocity becomes zero.

`v'^2=u'^2-2g.h`

`0^2=u'^2-2* 9.8* 5.3701`

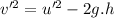
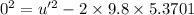
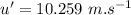`u'=10.259\ m.s^(-1)` is the initial velocity of tossing the apple.

Time taken to reach this height:

`v'=u'-g.t'`

`0=10.259-9.8* t'`

`t'=1.0469\ s`

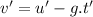
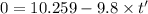
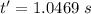
We observe that
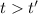`t>t'` hence the time after the launch of the projectile after which the apple should be tossed is:

`\Delta t=t-t'`

`\Delta t=1.0642-1.0469`

`\Delta t=0.0173\ s`