The three external forces acting on the system are the weights of the two children and the supporting force of the pivot.
Let us examine the torque produced by each. Torque is defined as
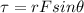
Here
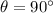 , so
, so
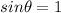 for all three forces.
for all three forces.
The torque exerted by three forces are
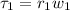
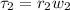
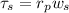
Now, the condition for equilibrium is that the sum of the torques on both children is zero, therefore
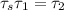
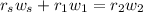
Weight (w) is mass times the acceleration due to gravity. Then
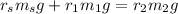
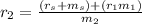
Replacing we have,

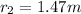
As expected, the heavier child must sit closer to the pivot to balance the seesaw.
PART B) We start considering the equilibrium in the system, then
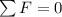
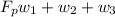
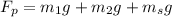
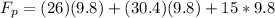
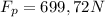
The supporting force exerted by the pivot is almost 700N