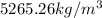Question

What is the average density of Venus if the acceleration due to gravity on its surface is 8.9 m/s2 and its radius is 6.05 106 m

Answer 1

To solve this problem we will apply the concept of gravity as a function of density, the universal gravity constant and the radius of the Planet to be investigated. This relationship is written mathematically as

`g = (4)/(3) \pi \rho GR`

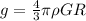
Here

G = Universal gravitational constant

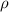`\rho` = Density

R = Radius

Given acceleration due to gravity on Venus's surface is

`g = 8.9m/s^2`

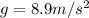
and Radius of Venus is

`R = 6.05*10^6m`

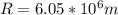
Using the previous equation and rearranging to find the density we have,

`\rho = (3g)/(4\pi GR)`

`\rho = (3(8.9))/((4\pi)(6.67*10^(-11))(6.05*10^6))`

`\rho = 5265.26kg/m^3`

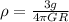
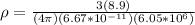
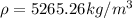
Therefore the average density of Venus is
`5265.26kg/m^3`