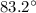Answer:
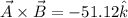
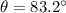
Step-by-step explanation:
We are given that
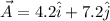

We have to find the scalar product and the angle between these two vectors

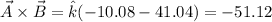
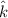
Angle between two vectors is given by

Where
 in degrees
in degrees

Using formula
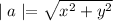
Where x= Coefficient of unit vector i
y=Coefficient of unit vector j
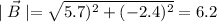

Using the formula
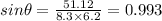
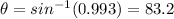 degrees
degrees
Hence, the angle between given two vectors=