Question

The desert temperature, H, oscillates daily between 40◦F at 5 am and 80◦F at 5 pm. Write a possible for- mula for H in terms of ????, measured in hours from 5 am.

Answer 1

`H(t)=-20\text{cos}((\pi)/(12)t)+60`

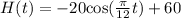
Explanation:

We have been given that the desert temperature, H, oscillates daily between 40◦F at 5 am and 80◦F at 5 pm. We are asked to write a formula H in terms of t, measured in hours from 5 am.

We will use cosine function to write our required formula.

`y=A\text{cos}[B(x-C)]+D`, where,

A = Amplitude,

`\text{Period}=(2\pi)/(|B|)`

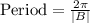
C = Phase shift,

D = Vertical shift.

First of all, we will find amplitude using maximum and minimum values as:

`A=\frac{\text{Maximum value}-\text{Minimum value}}{2}`

`A=(80-40)/(2)`

`A=(40)/(2)`

`A=20`

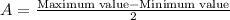
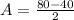
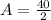
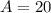
Since period is 24 hours (5 am to 5 pm), so let us find B as:

`24=(2\pi)/(|B|)`

`B=(2\pi)/(24)`

`B=(\pi)/(12)`

`\text{Vertical shift}=\frac{\text{Maximum value}+\text{Minimum value}}{2}`

`D=(80+40)/(2)=(120)/(2)=60`

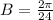
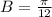
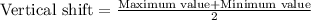
There is no phase shift.

Since temperature is minimum when
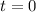`t=0`, so we will use negative cosine as:

`H(t)=-20\text{cos}((\pi)/(12)t)+60`

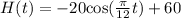
Therefore, our required function would be
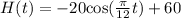`H(t)=-20\text{cos}((\pi)/(12)t)+60`.