Question

1.44 Make-up exam: In a class of 28 students, 27 of them took an exam in class and 1 student took a make-up exam the following day. The professor graded the first batch of 27 exams and found an average score of 79 points with a standard deviation of 6.5 points. The student who took the make-up the following day scored 63 points on the exam.

a) Does the new student's score increase or decrease the average?
Decreases
Increases
b) The new average is: (round to two decimal places)
c) Does the new student's score increase or decrease the standard deviation of the scores?
Decreases
Increases

Answer 1

a) Decrease

b) New mean = 78.43

c) Decrease

Explanation:

We are given the following in the question:

Total number of students in class = 28

Average of 27 students = 79

Standard Deviation of 27 students = 6.5

New student's score = 63

a) The new student's score will decrease the average.

b) New mean

`Mean = \displaystyle\frac{\text{Sum of all observations}}{\text{Total number of observation}}`

`Mean = (\displaystyle\sum x_i)/(27) = 79\\\\\sum x_i = 27* 79 = 2133`

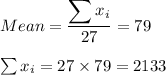
New mean =

`\text{ New mean} =( \displaystyle\sum x_i +63)/(28)\\\\ =(2133+63)/(28)= (2196)/(28) = 78.43`

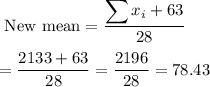
Thus, the new mean is 78.43

c) Since the new mean decreases, standard deviation for new scores will decrease.

This is because the new value is within the usual values i.e. within two standard deviations of the mean. So, this wont cause a lot of variation as this value will be closer to already available data values. Also number of observations (n) in the denominator is increasing. Based on both these points we can conclude that standard deviation will decrease

Formula for Standard Deviation:

`\text{Standard Deviation} = \sqrt{\displaystyle\frac{\sum (x_i -\bar{x})^2}{n}}`

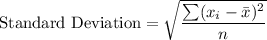
where
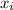`x_i` are data points,
`\bar{x}` is the mean and n is the number of observations.