Question

Which graph represents h(x)?

Answer 1

Explanation:

B

Answer 2

There is only graph that starts with a line from y = h(x) = -4. Hence the required graph of the plot of h(x) is given by the second graph.

Therefore the correct option is the second graph.

Explanation:

i) h(x) =
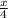`(x)/(4)` - 4 for x ≤ 0. Therefore when x = 0 h(x) = -4

There is only graph that starts with a line from y = h(x) = -4. Hence the required graph of the plot of h(x) is given by the second graph.

ii) For x < 0 we see from the from the equation in i) that h(x) will be more and more negative as the value of x decreases from 0.

iii) h(x) =
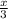`(x)/(3)` - 3 for 0 < x ≤ 3 . Therefore when x = 0 , h(x) = -3 and again when x = 3 then x = -2 which is again the condition fulfilled by graph 2.

iv) h(x) =
`(x)/(2)` - 2 for x ≥ 4 . Therefore when x = 4 h(x) = 0 and as x increases from 4 we see that h(x) also increases to positive values.

This is also satisfied in the plot shown in the second graph.

v) Therefore the correct option is the second graph.