Question

Problem A. Consider the following initial value problem for a damped driven linear oscillator: m 2 + b** + kx} = f sin(St); x(0) = a, x'(0) = C, where a,b,c, m, k, f, 12 are constants, and [m] = M, [t] = T, [2] = L. Find the dimensions of a,b,c, k, ſ, and 12.

Answer 1

a = L

b = MT^(-1)

c = LT^(-1)

k = MT^(-2)

f = MLT^(-2)

S = T^(-1)

Explanation:

x (0) = a

x is denoted by displacement in vibration analysis hence attains units of x.

Hence, a = L

b is the damping coefficient:

`b = (F)/((dx)/(dt) ) \\= MLT^(-2) / LT^(-1)\\= MT^(-1)`

x'(0) = c

dx/dt = velocity hence c attains the units of velocity

c = LT^(-1)

Coefficient k is the stiffness:

`k = (F)/(x) = (MLT^(-2))/(L) = MT^(-2)`

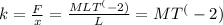
Coefficient f is the magnitude of the exciting force

`F = m*acceleration = MLT^(-2)`

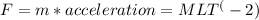
Coefficient S is the angular frequency

angular frequency is displacement in radians per seconds; hence,

S = T^(-1)