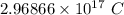Question

If an evil genius decided to free the Earth from the Sun by charging both (with an equal charge) to generate an electrical force equal to the gravitational force between them, how much charge would be needed on each?

Answer 1

`2.96866* 10^(17)\ C`

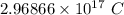
Step-by-step explanation:

G = Gravitational constant = 6.67 × 10⁻¹¹ m³/kgs²

k = Coulomb constant =
`8.99* 10^(9)\ Nm^2/C^2`

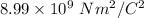
r = Distance between the objects and particles

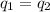`q_1=q_2` = Charges

M = Mass of Sun =
`1.989* 10^(30)\ kg`

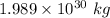
m = Mass of Earth =
`5.972* 10^(24)\ kg`

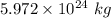
Here, the Electric force will balance the gravitational force

`(GMm_2)/(r^2)=(kq_1q_2)/(r^2)\\\Rightarrow q=\sqrt{(GMm)/(k)}\\\Rightarrow q=\sqrt{(6.67* 10^(-11)* 5.972* 10^(24)* 1.989* 10^(30))/(8.99* 10^(9))}\\\Rightarrow q=2.96866* 10^(17)\ C`

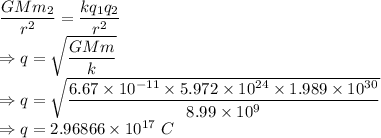
Charge on each particle will be
`2.96866* 10^(17)\ C`