Answer:
Option C. As x approaches positive infinity, f(x) approaches positive infinity, and g(x) approaches negative infinity.
Explanation:
we know that
Observing the table
The function f(x) is a increasing function
As the value of x increases, the value of f(x) increases
so
As x approaches positive infinity, f(x) approach positive infinity
Find the slope of the linear equation g(x)
The formula to calculate the slope between two points is equal to
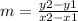
we have the points (6, -2) and (3, 7)
substitute
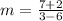
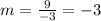
The slope of the linear equation g(x) is negative
That means ----> Is a decreasing function
As the value of x increases, the value of g(x) decreases
so
As x approaches positive infinity, g(x) approach negative infinity
therefore
As x approaches positive infinity, f(x) approaches positive infinity, and g(x) approaches negative infinity.