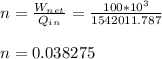Question

Water is the working fluid in an ideal Rankine cycle. The condenser pressure is 8 kPa, and saturated vapor enters the turbine at (a) 18 MPa and (b) 4 MPa. The net power output of the cycle is 100 MW.

Determine for each case a) the mass flow rate of steam, in kg/h, b) the heat transfer rates for the working fluid passing through the boiler and condenser, each in kW, and c) the thermal efficiency.

Answer 1

Step-by-step explanation:

The obtained data from water properties tables are:

Point 1 (condenser exit) @ 8 KPa, saturated fluid

`h_(f) = 173.358 \\h_(fg) = 2402.522`

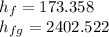
Point 2 (Pump exit) @ 18 MPa, saturated fluid & @ 4 MPa, saturated fluid

`h_(2a) = 489.752\\h_(2b) = 313.2`

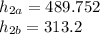
Point 3 (Boiler exit) @ 18 MPa, saturated steam & @ 4 MPa, saturated steam

`h_(3a) = 2701.26 \\s_(3a) = 7.1656\\h_(3b) = 2634.14\\s_(3b) = 7.6876`

Point 4 (Turbine exit) @ 8 KPa, mixed fluid

`x_(a) = 0.8608\\h_(4a) = 2241.448938\\x_(b) = 0.9291\\h_(4b) = 2405.54119`

Calculate mass flow rates

Part a) @ 18 MPa

mass flow

`(100*10^6 )/(w_(T) - w_(P)) = (100*10^3 )/((h_(3a) - h_(4a)) - (h_(2a) - h_(f)))\\\\= (100*10^ 3)/((2701.26 - 2241.448938 ) - (489.752 - 173.358))\\\\= 697.2671076 (kg)/(s) = 2510161.587 (kg)/(hr)`

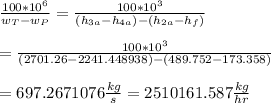
Heat transfer rate through boiler

`Q_(in) = mass flow * (h_(3a) - h_(2a))\\Q_(in) = (697.2671076)*(2701.26-489.752)\\\\Q_(in) = 1542011.787 W`

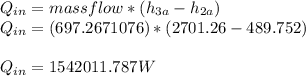
Heat transfer rate through condenser

`Q_(out) = mass flow * (h_(4a) - h_(f))\\Q_(out) = (697.2671076)*(2241.448938-173.358)\\\\Q_(out) = 1442011.787 W`

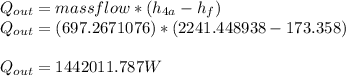
Thermal Efficiency

`n = (W_(net) )/(Q_(in) ) = (100*10^3)/(1542011.787) \\\\n = 0.06485`

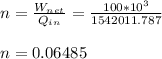
Part b) @ 4 MPa

mass flow

`(100*10^6 )/(w_(T) - w_(P)) = (100*10^3 )/((h_(3b) - h_(4b)) - (h_(2b) - h_(f)))\\\\= (100*10^ 3)/((2634.14 - 2405.54119 ) - (313.12 - 173.358))\\\\= 1125 (kg)/(s) = 4052374.235 (kg)/(hr)`

Heat transfer rate through boiler

`Q_(in) = mass flow * (h_(3b) - h_(2b))\\Q_(in) = (1125.65951)*(2634.14-313.12)\\\\Q_(in) = 2612678.236 W`

Heat transfer rate through condenser

`Q_(out) = mass flow * (h_(4b) - h_(f))\\Q_(out) = (1125)*(2405.54119-173.358)\\\\Q_(out) = 2511206.089 W`

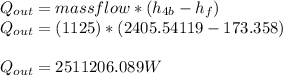
Thermal Efficiency

`n = (W_(net) )/(Q_(in) ) = (100*10^3)/(1542011.787) \\\\n = 0.038275`