Question

A photographer stands 60 yards from the base of a lighthouse and observes that the angle between the ground and the top of the lighthouse is 41°. How tall is the lighthouse?

Answer 1

52.2

Explanation:

It was correct on my assignment

Answer 2

The height of lighthouse is 52.2 yards

Solution:

Given that photographer stands 60 yards from the base of a lighthouse and observes that the angle between the ground and the top of the lighthouse is 41 degree

The diagram is attached below

Consider a right angled triangle ABC

AB is the height of the lighthouse

BC is the distance between the base of a lighthouse and Photographer

As per given, BC = 60 yards

Angle between the ground and the top of the lighthouse is 41 degree

Angle ACB = 41 degree

To find: height of lighthouse i.e AB = ?

We know that,

`tan(\angle ACB) = (Perpendicular)/(Base)`

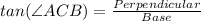
Here Base is BC and perpendicular is AB

`\tan 41^(\circ)=(A B)/(B C)`

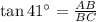
Substituting the values,

`\begin{aligned}&\tan 41^(\circ)=(A B)/(60)\\\\&0.8692=(A B)/(60)\\\\&A B=0.8692 * 60=52.157 \approx 52.2\end{aligned}`

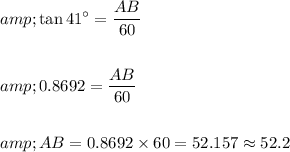
Thus the height of lighthouse is 52.2 yards