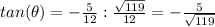Question

Suppose that ? Is an angle with csc(?)=-12/5 and ? Is not in the third quadrant. Compute the exact value of Tan(?). You don’t have to rationalize the denominator.

I think the answer is -5/rad119, but I’m not sure

Answer 1

`tan(\theta)=-(5)/(√(119))`

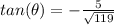
Explanation:

The correct question is

Suppose that ∅ Is an angle with csc(∅)=-12/5 and ∅ Is not in the third quadrant. Compute the exact value of Tan(∅).

∅ Is not in the third quadrant

If csc(∅) is negative the angle lie in the III Quadrant or in the IV Quadrant

∅ Is not in the third quadrant ----> given problem

so

That means ----> ∅ Is in the fourth quadrant

step 1

Find the value of
`sin(\theta)`

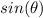
we have

`csc(\theta)=-(12)/(5)`

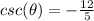
we know that

`csc(\theta)=(1)/(sin(\theta))`

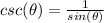
therefore

`sin(\theta)=-(5)/(12)`

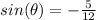
step 2

Find the value of
`cos(\theta)`

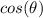
we know that

`sin^2(\theta)+cos^2(\theta)=1`

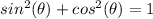
we have

`sin(\theta)=-(5)/(12)`

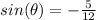
substitute

`(-(5)/(12))^2+cos^2(\theta)=1`

`(25)/(144)+cos^2(\theta)=1`

`cos^2(\theta)=1-(25)/(144)`

`cos^2(\theta)=(119)/(144)`

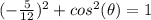
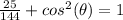
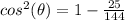
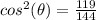
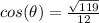`cos(\theta)=(√(119))/(12)` ---> is positive (IV Quadrant)

step 3

Find the value of
`tan(\theta)`

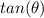
we know that

`tan(\theta)=(sin(\theta))/(cos(\theta))`

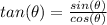
substitute the values

`tan(\theta)=-(5)/(12) : (√(119))/(12)=-(5)/(√(119))`