Question

An admiral, captain, and commander, all different, are to be chosen from a group of 10 Starfleet officers. How many different choices of officers are possible if (a) there are no restrictions? (b) Worf and Troi will not serve together?

Answer 1

720 different choices of officers are possible if there are no restrictions.

The number of ways in which Worf and Troi will not serve together is 672.

Step-by-step explanation:

Consider the provided information.

We have 3 post admiral, captain, and commander, and 10 Starfleet officers.

Part (A) there are no restrictions?

We need to select 3 people out of 10. And these 3 people can again rearranged into different rank.

Thus, the number of ways are:
`(^(10)C_3)3!=\left((10!)/(3!7!)\right)3!=720`

Hence, 720 different choices of officers are possible if there are no restrictions.

Part (B) Worf and Troi will not serve together?

Subtract those cases in which both of them are selected from total number of ways.

If both of them selected then we need to select only 1 person out of 8. And further they can rearranged into 3 different rank.

Thus, the number of ways are:
`720-(^(8)C_1)3!=720-8*3!=672`

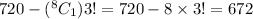
Hence, the number of ways in which Worf and Troi will not serve together is 672.