Question

A supermarket has determined that daily demand for milk containers has an approximate bell shaped distribution, with a mean of 55 containers and a standard deviation of six containers. How often can we expect between 49 and 61 containers to be sold in a day?

Answer 1

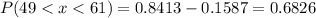`\\ P(49<x<61) = 0.8413 - 0.1587 = 0.6826` or 68.26%.

Explanation:

The daily demand for milk containers has a Normal (or Gaussian) distribution, and we can use values from the cumulative distribution function and z-scores to solve the question.

We know from the question that the mean of the distribution is:

`\\ \mu = 55`

And a standard deviation of:

`\\ \sigma = 6`

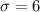
The z-scores permit calculates the probabilities for any case whose values have a Normal o Gaussian distribution. Then, for this, we need to calculate the z-scores for 49 containers and 61 containers to establish the corresponding probabilities, as well as the differences between these two values to determine the probability between them.

These z-scores are given by:

`\\ z = (x-\mu)/(\sigma)`

Thus,

The z-scores for 49 and 61 containers are:

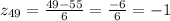`\\ z_(49) = (49 - 55)/(6) = (-6)/(6) = -1` [1]

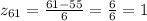`\\ z_(61) = (61 - 55)/(6) = (6)/(6) = 1` [2]

Well, this is a special case when in both cases the values are one standard deviation from the mean, but in one case (
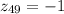`\\ z_(49) = -1`) the values are smaller than the mean and in the other case (
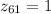`\\ z_(61) = 1`) the values are greater than the mean.

In other words, the cumulative probability for (
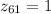`\\ z_(61) = 1`), obtained from any Table of the Normal Distribution available on the Web, is: 0.8413 (or 84.13%) and the cumulative probability for (
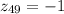`\\ z_(49) = -1`) is: 1 - 0.8413 = 0.1587 (or 15.87%), because of the symmetry of the Normal Distribution.

Then, the probability of expecting to sell between 49 and 61 containers in a day is the difference of both obtained probabilities:

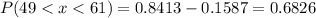`\\ P(49<x<61) = 0.8413 - 0.1587 = 0.6826` or 68.26%.

See the graph below.