Answer:
The probability that he picked 2 purpled socks is 0.33.
Explanation:
Given:
Number of purple socks,
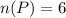
Number of orange socks,
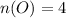
Two socks are picked without replacement.
Now, total number of socks,
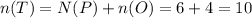
Probability of picking the first cap as purple cap is given as:
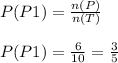
Since there is no replacement, the number of socks decreases by 1. Also, if the first sock picked is purple, then number of purple socks is also decreased by 1.
Therefore, probability of picking the second cap as purple cap is given as:
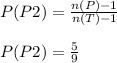
Now, probability that both the picked caps are purple is given by their probability product. This gives,
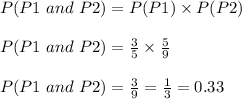
Therefore, the probability that he picked 2 purpled socks is 0.33