Answer:
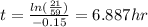
So it would takes approximately 6.9 hours to reach 32 F.
Step-by-step explanation:
For this case we have the following differential equationÑ
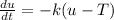
We can reorder the expression like this:
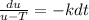
We can use the substitution
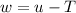 and
and
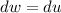 so then we have:
so then we have:
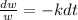
IF we integrate both sides we got:
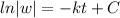
If we apply exponential in both sides we got:
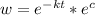
And if we replace w = u-T we got:
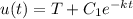
We can also express the solution in the following terms:
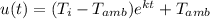
For this case we know that
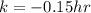 since w ehave a cooloing,
since w ehave a cooloing,
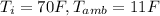 , we have this model:
, we have this model:
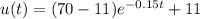
And if we want that the temperature would be 32F we can solve for t like this:
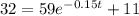
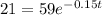
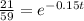
If we apply natural logs on both sides we got:
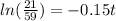
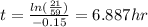
So it would takes approximately 6.9 hours to reach 32 F.