Question

Newton's law of cooling is:

du/dt= -k(u-T)

where u(t) is temperature of an object, t is in hours, T is a constant ambient temperature, and k is a positive constant.

Suppose a building loses heat in accordance with Newton's law of cooling. Suppose that the rate constant k has the value 0.15 hr ? 1 . Assume that the interior temperature is Ti = 70?F, when the heating system fails. If the external temperature is T = 11? F, how long will it take for the interior temperature to fall to T1 = 32?F?

Answer 1

The interior temperature of the building will take approximately 3 hours and 10 minutes to fall to 32°F.

Step-by-step explanation:

To find out how long it will take for the interior temperature of the building to fall to 32°F, we can use Newton's law of cooling equation du/dt = -k(u-T). We are given that the rate constant

`k = 0.15 hr^(-1)`

, the initial temperature u(0) = 70°F, the ambient temperature T = 11°F, and the final temperature T1 = 32°F.

We can rearrange the equation to solve for u(t): du/(u-T) = -k dt. Integrating both sides from u(0) to u(t) and from 0 to t, we get ln((u(t)-T)/(u(0)-T)) = -kt. Substituting the known values, we can solve for t: ln((32-11)/(70-11)) = -0.15t. Simplifying, we find t = 3.173 hours, or approximately 3 hours and 10 minutes.

Answer 2

`t = (ln((21)/(59)))/(-0.15)=6.887 hr`

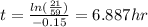
So it would takes approximately 6.9 hours to reach 32 F.

Step-by-step explanation:

For this case we have the following differential equationÑ

`(du)/(dt)= -k (u-T)`

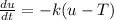
We can reorder the expression like this:

`(du)/(u-T) = -k dt`

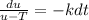
We can use the substitution
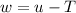`w = u-T` and
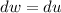`dw =du` so then we have:

`(dw)/(w) =-k dt`

IF we integrate both sides we got:

`ln |w| = -kt +C`

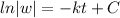
If we apply exponential in both sides we got:

`w = e^(-kt) *e^c`

And if we replace w = u-T we got:

`u(t)= T + C_1 e^(-kt)`

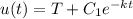
We can also express the solution in the following terms:

`u(t) = (T_i -T_(amb)) e^(kt) +T_(amb)`

For this case we know that
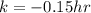`k =-0.15 hr` since w ehave a cooloing,
`T_(i)= 70 F, T_(amb)=11F`, we have this model:

`u(t) = (70-11) e^(-0.15t) +11`

And if we want that the temperature would be 32F we can solve for t like this:

`32 = 59 e^(-0.15 t) +11`

`21=59 e^(-0.15 t)`

`(21)/(59) = e^(-0.15 t)`

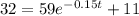
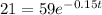
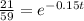
If we apply natural logs on both sides we got:

`ln ((21)/(59)) =-0.15 t`

`t = (ln((21)/(59)))/(-0.15)=6.887 hr`

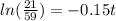
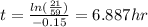
So it would takes approximately 6.9 hours to reach 32 F.