Question

Roxanne is planning to enclose her right triangular shaped garden with a fence. How many

feet of fencing does she need to enclose her entire garden if the length of her garden
measures 19 feet and the hypotenuse of her garden measures 33 feet? Round your answer to
the nearest tenth of a foot.
**Remember... to find the perimeter of an object, you must ADD the lengths of all sides.

Answer 1

The perimeter of Roxanne's right triangular garden is 79 feet.

Explanation:

Given,

Length of 1 side = 19 feet

Hypotenuse = 33 feet

We have to find out the perimeter of the triangular garden.

Solution,

Since the garden is in shape of right triangle.

So we apply the Pythagoras theorem to find the third side.

"In a right angled triangle the square of the hypotenuse is equal to the sum of the squares of the other two sides".

So framing in equation form, we get;

`33^2=19^2+(third\ side)^2\\\\1089=361+(third\ side)^2\\\\(third\ side)^2=1089-361\\\\(third\ side)^2=728`

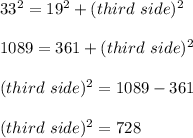
Now taking square root on both side, we get;

`√((third\ side)^2) =√(728) \\\\third\ side=26.98\approx27\ ft`

Now we know that the perimeter is equal to sum of all the three side of a triangle.

Perimeter =
`19+27+33=79\ ft`

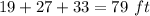
Hence The perimeter of Roxanne's right triangular garden is 79 feet.