Question

A 4.60 gg coin is placed 19.0 cmcm from the center of a turntable. The coin has static and kinetic coefficients of friction with the turntable surface of μs = 0.820 and μk = 0.440. The turntable very slowly speeds up.1. What is the angular speed in rpm when the coin slides off?

Answer 1

62.64 RPM.

Step-by-step explanation:

Given that

m= 4.6 g

r= 19 cm

μs = 0.820

μk = 0.440.

The angular speed of the turntable = ω rad/s

Condition just before the slipping starts

The maximum value of the static friction force =Centripetal force

`\mu_s\ m g=m\ \omega^2\ r\\ \omega^2=(\mu_s\ m g)/(m r)\\ \omega=\sqrt{(\mu_s\ g)/( r)}\\ \omega=\sqrt{(0.82* 10)/( 0.19)}\ rad/s\\\omega= 6.56\ rad/s`

`\omega=(2\pi N)/(60)\\N=(60* \omega)/(2\pi )\\N=(60* 6.56)/(2\pi )\ RPM\\N=62.64\ RPM`

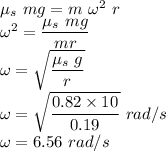
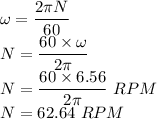
Therefore the speed in RPM will be 62.64 RPM.