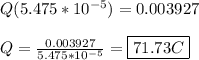Question

The magnetic field perpendicular to a single wire loop of diameter 10.0 cm decreases from 0.50 T to zero. The wire is made of copper and has a diameter of 2.0 mm and length 1.0 cm. How much charge moves through the wire while the field is changing?

I know how to do the calculations, but can someone please explain what is the 10cm diameter and 2mm diameter? Why is there one wire and two diameters? I understand this problem mathematically but not conceptually.

Answer 1

Hi there!

We can begin by using Lenz's Law:

`\epsilon = -N(d\Phi _B)/(dt)`

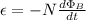
N = Number of Loops

Ф = Magnetic Flux (Wb)
t = time (s)

Also, we can rewrite this as:

`\epsilon = -NA(dB)/(dt)`

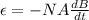
A = Area (m²)

Since the area is constant, we can take it out of the derivative.

This is a single wire loop, so N = 1.

Now, we can develop an expression for the induced emf.

We can begin by solving for the area:

`A = \pi r^2 \\\\d = r/2 r = 0.05cm \\\\A = \pi (0.05^2) = 0.007854 m^2`

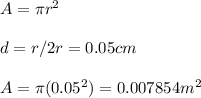
We can also express dB/dt as:

`(dB)/(dt) = (\Delta B)/(t) = (0-0.5)/(t) = (-0.5)/(t)`

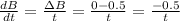
Now, we can create an equation.

`\epsilon = -(1)(0.007854)(-0.5)/(t) = (0.003927)/(t)`

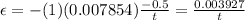
To solve the system, we must now develop an expression for current given an emf and resistance.

Begin by calculating the resistance of the copper wire:

`R = (\rho L)/(A)`

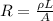
ρ = Resistivity of copper (1.72 * 10⁻⁸ Ωm)
L = Length of wire (0.01 m)

A = cross section area (m²)

Solve:

`R = ((1.72*10^(-8))(0.01))/(\pi (0.001^2)) = 5.475 * 10^(-5) \Omega m`

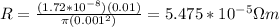
Now, we can use the following relation (Ohm's Law):

`\epsilon = iR\\\\\epsilon = (Q)/(t)R`

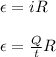
*Since current is equivalent to Q/t.

Plug in the value of R and set the two equations equal to each other.

`(Q)/(t)(5.475 * 10^(-5)) = (0.003927)/(t)`

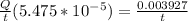
Cancel out 't'.

`Q (5.475 * 10^(-5)) = 0.003927 \\\\Q = (0.003927)/(5.475*10^(-5)) = \boxed{71.73 C}`