Question

What function do you know from calculus is such that its first derivative is a constant multiple k of itself

Answer 1

Exponential function if the form
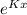`e^(Kx)` is the constant multiple K of itself if.

`y'=(dy)/(dx)=cKe^(Kx) \\y'=Ky`

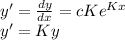
Explanation:

The exponential function of the form
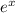`e^x` is the function which is the derivative of itself.

Where:

x is independent variable

Now if we talk about constant then again exponential function if the form
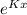`e^(Kx)` is the constant multiple K of itself if we take the dervative.

Mathmatical Prove:

Consider the general equation

let
`y=ce^(Kx)`

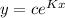
Where:

K is a constant

c is the cofficient(could be any number)

Now:

Taking derivative of above equation w.r.t x:

`y'=(dy)/(dx)=cKe^(Kx) \\y'=Ky`

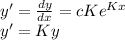
Hence proved exponential function is a constant multiple K of it self.