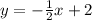Question

A line contain the point (2,1) and (0,2) what is the equation of the line

Answer 1

Slope-intercept form is y = mx + b

[m is the slope, b is the y-intercept or the y value when x = 0 ---> (0, y) or the point where the line crosses through the y-axis]

To find the slope, use the slope formula:

`m=(y_2-y_1)/(x_2-x_1)` Plug in the two points into the equation

(2, 1) ---> (x₁, y₁)

(0, 2) ---> (x₂, y₂)

`m = (y_2-y_1)/(x_2-x_1)`

`m=(2-1)/(0-2)`

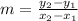
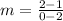
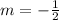`m=-(1)/(2)` Now that you have the slope, plug it in:

y = mx + b

y = -1/2x + b To find b, plug in one of the points. I will use (0, 2)

2 = -1/2(0) + b

2 = b Now plug it in:

`y=-(1)/(2)x+2`

Answer 2

Answer: y = -x/2 + 2

Explanation:

The equation of a line given two points , is calculated by the formula :

`(y-y_(1))/(x - x_(1))` =
`(y_(2)-y_(1))/(x_(2)-x_(1))`

`x_(1)` = 2

`x_(2)` = 0

`y_(1)` = 1

`y_(2)` = 2

substituting the values , we have

`(y-1)/(x-2)` =
`(2-1)/(0-2)`

`(y-1)/(x-2)` =
`(1)/(-2)`

-2(y-1) = x-2

-2y + 2 = x - 2

-2y = x - 2 - 2

-2y = x - 4

writing the equation in slope intercept form , we have

y = -x/2 + 2