Question

It is known that 45% of senior citizens are deficient in vitamin D. Let Y be the number of vitamin D efficient individuals in a random sample of n = 15 senior citizens. (a) Calculate P(Y = 5). Also obtain an approximation for this probability using the normal approximation. (b) Calculate P(Y > 7). Also obtain normal approximations for this probability with and without using continuity correction. (c) Calculate P(4

Answer 1

a ) 0.1403604645 and 0.1368

b) 0.3464961 and 0.3485

c) 0.802671982 and 0.8018

Explanation:

Y~ B (15,0.45)

Y~ N (15*0.45, 15*0.45*0.55) = Y~ N (6.75, 3.7125)

a) P(Y=5) = 15C5 (0.45)^5 * (0.55)^10 = 0.1403604645

For normal approximation

P(Y = 5 ) = P ( 4.5 < Y < 5.5 ) ......... continuity correction

Hence,

`P ( 4.5 < Y < 5.5 ) = P ( (4.5 - 6.75)/(√(3.7125) ) < Z < (5.5 - 6.75)/(√(3.7125) ) ) = P ( -1.16775 < Z < -0.64875 )`

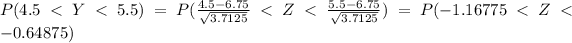
The probability P ( 4.5 < Y < 5.5 ) = 0.1368

b) P(Y>7) = 15C8 (0.45)^ 8 (0.55)^7 + 15C9 (0.45)^9 * (0.55)^6 + 15C10 (0.45)^10 * (0.55)^5 + 15C11 (0.45)^11 * (0.55)^4 + 15C12 (0.45)^12 * (0.55)^3 + 15C13 (0.45)^13 * (0.55)^2 + 15C14 (0.45)^14 * (0.55) + (0.45)^15

= 0.3464961

For normal approximation

P(Y > 7 ) = P (Y > 7.5 ) ......... continuity correction

Hence,

`P (Y > 7.5) = P (Z > (7.5-6.75)/(√(3.7125) ) ) = P (Z > 0.389249)\\`

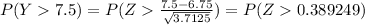
The probability P ( Y>7.5 ) = 0.3485

c) P (4 < Y < 10) = 15C5 (0.45)^5 (0.55)^10 + 15C6 (0.45)^ 6 (0.55)^9 + 15C7 (0.45)^7 (0.55)^8 + 15C8 (0.45)^ 8 (0.55)^7 + 15C9 (0.45)^9 * (0.55)^6

= 0.802671982

For normal approximation

P( 4 < Y < 10 ) = P (4.5< Y < 9.5 ) ......... continuity correction

Hence,

`P ( 4.5 < Y < 9.5 ) = P ( (4.5 - 6.75)/(√(3.7125) ) < Z < (9.5 - 6.75)/(√(3.7125) ) ) = P ( -1.167748416 < Z < 1.427248064 )`

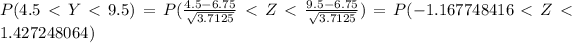
The probability P (4.5< Y < 9.5 ) = 0.8018