Question

A communications circuit is known to have an availability of 0.99 (that is, 99% of the time, the circuit is operational). A total of n such circuits are going to be set up by the FAA between San Francisco and Los Angeles in such a way that the circuits will fail indepen- dently of each other. How many such parallel circuits must be set up to attain an overall availabililty of 0.99999

Answer 1

Assume that for the communication to be available means that at least one of the
`n` circuits is operational. It would take at least 3 circuits to achieve a
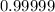`0.99999` overall availability.

Explanation:

The probability that one circuit is not working is
`1 - 0.99 = 0.01`.

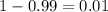Since the circuits here are all independent of each other, the probability that none of them is working would be
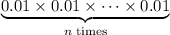`\displaystyle \underbrace{0.01 * 0.01 * \cdots * 0.01}_{\text{$n$ times}}`. That's the same as
`0.01^n`.

The event that at least one of the
`n` circuits is working is the complement of the event that none of them is working. To find the probability that at least one of the
`n` circuits is working, simply subtract the probability that none of the circuit is working from one. That is:

`\begin{aligned}&P(\text{At least one working}) \cr &= 1 - P(\text{None is working}) \cr &= 1- 0.01^n\end{aligned}`.

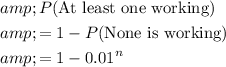The question requests that

`P(\text{At least one working}) \ge 0.99999`.

In other words,

`1- 0.01^n \ge 0.99999`.

`0.01^n \le 1 - 0.99999 = 0.000001 = 10^(-6)`.

Note that
`0.01 = 10^(-2)`. Hence, the inequality becomes

`\left(10^(-2)\right)^n \le 10^(-6)`.

`10^(-2\,n) \le 10^(-6)`

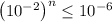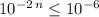
Take the natural log of both sides of the equation:

`\ln\left(10^(-2\, n)\right) \le \ln \left(10^(-6)\right)`.

`(-2\, n)\ln\left(10\right) \le (-6) \ln\left(10\right)`.

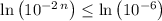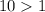`10 > 1`, hence
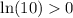`\ln(10) > 0`. Divide both sides by
`\ln(10)`:

`-2\,n \le -6`.

`n \ge 3`.

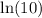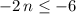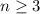In other words, at least three parallel circuits must be set up to achieve that availability.