Answers:
a)The balloon is 68 m away of the radar station
b) The direction of the balloon is towards the radar station
Step-by-step explanation:
We can solve this problem with the Doppler shift equation:
 (1)
(1)
Where:
 is the actual frequency of the sound wave
is the actual frequency of the sound wave
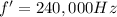 is the "observed" frequency
is the "observed" frequency
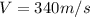 is the velocity of sound
is the velocity of sound
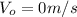 is the velocity of the observer, which is stationary
is the velocity of the observer, which is stationary
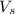 is the velocity of the source, which is the balloon
is the velocity of the source, which is the balloon
Isolating
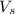 :
:
 (2)
(2)
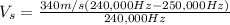 (3)
(3)
 (4) This is the velocity of the balloon, note the negative sign indicates the direction of motion of the balloon: It is moving towards the radar station.
(4) This is the velocity of the balloon, note the negative sign indicates the direction of motion of the balloon: It is moving towards the radar station.
Now that we have the velocity of the balloon (hence its speed, the positive value) and the time (
 ) given as data, we can find the distance:
) given as data, we can find the distance:
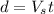 (5)
(5)
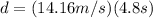 (6)
(6)
Finally:
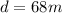 (8) This is the distance of the balloon from the radar station
(8) This is the distance of the balloon from the radar station