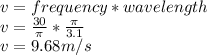Question

The displacement of a wave traveling in the negative y-direction is D(y,t) = ( 4.60 cm ) sin ( 6.20 y+ 60.0 t ), where y is in m and t is in s?

Answer 1

The question is incomplete, below is the complete question

"The displacement of a wave traveling in the negative y-direction is D(y,t) = ( 4.60cm ) sin ( 6.20 y+ 60.0 t ), where y is in m and t is in s.

A) What is the frequency of this wave?

B) What is the wavelength of this wave?

C) What is the speed of this wave?"

Answers:

a.
`f=(30)/(\pi )Hz\\`

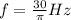
b.
`wavelength=(\pi )/(3.1)m \\`

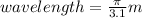
c.
`v=9.68m/s`

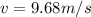
Step-by-step explanation:

The equation of a wave is represented as

`D(x,t)=Asin(kx+wt) \\`

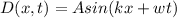
Where A=amplitude

w=angular frequency=2πf

K=wave numbers =2π/λ

since we re giving he equation D(y,t) = ( 4.60cm ) sin ( 6.20 y+ 60.0 t ),

we can compare and get the value for the wave number and angular frequency.

By comparing we have

w=60rads/s

k=6.20

a. to determine the frequency, from the expression fr angular wave frequency we have

w=2πf hence

f=w/2π

if we substitute we arrive at

`f=(60)/(2\pi )\\f=(30)/(\pi )Hz\\`

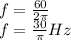
b. to determine the wave length, we use

`k=(2\pi )/(wavelength) \\k=6.2\\wavelength=(2\pi )/(k) \\wavelength=(2\pi )/(6.2) \\wavelength=(\pi )/(3.1)m \\`

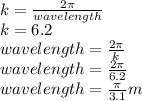
c. the wave speed v is express as the product of the frequency and the wavelength. Hence

`v=frequency*wavelength \\v=(30)/(\pi ) *(\pi )/(3.1)\\ v=9.68m/s`