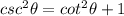Question

2.) Fill in the blank.

csc^2 0 = cot ^2 0 + ___
A.) sec ^2 0
B.) -cos ^2 0
C.) -tan ^2 0
D.) 0
E.) 1

Answer 1

E.) 1

Explanation:

Firstly we will solve for L.H.S.

L.H.S. =
`Csc^2\theta`

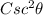
Since we know that
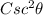`Csc^2\theta` is the inverse of
`Sin^2\theta`.

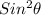So we can say that;

`csc^2\theta=(1)/(sin^2\theta)`

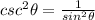
Now For R.H.S.

`Cot^2\theta+1`

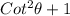
Since we can rewrite
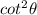`cot^2\theta` as
`(cos^2\theta)/(sin^2\theta)`.

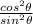Now we can say that the R.H.S. is;

`(cos^2\theta)/(sin^2\theta)+1`

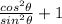
Now we add the fraction and get;

`(cos^2\theta+sin^2\theta)/(sin^2\theta)`

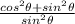
Now according to trigonometric identity;

`cos^2\theta+sin^2\theta=1`

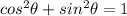
So,
`(cos^2\theta+sin^2\theta)/(sin^2\theta)=(1)/(sin^2\theta)`

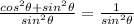
Here,

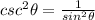`csc^2\theta=(1)/(sin^2\theta)` and
`Cot^2\theta+1` =
`(1)/(sin^2\theta)`

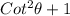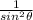
L.H.S. = R.H.S.

Hence
`csc^2\theta=cot^2\theta+1`