Question

Which of these strategies would eliminate a variable in the system of equations?

10x+4y=-2
5x-2y=2

Answer 1

A AND B IS THE CORRECT ANSWER

Explanation:

I JUST TOOK THE TEST :)

Answer 2

Option A: Multiply the top equation by
`$ \frac{\textbf{1}}{\textbf{2}} $`, then add the equations.

Explanation:

OPTION A:

When we multiply the top equation by
`$ (1)/(2) $` we get:

`$ (1)/(2)10x + (1)/(2)4y = (1)/(2)(-2) $`

`$ = 5x + 2y = -1 $`

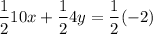
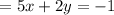
Now, we add the second equation to this, we get:

5x + 2y + 5x - 2y = -1 + 2

`$ \implies 10x = 1 $`

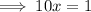
The 'y' variable is eliminated.

OPTION B: Note that multiplying the second equation by 2 would result in:

10x - 4y = 4. To eliminate 'y' we should add this equation to the top equation not subtract it. So, this option is wrong.

OPTION C:

Adding the equations also will result in a equation of two variables, viz:

15x + 2y = 0 which does not eliminate any variable at all.

So, OPTION C is also wrong.

Hence, OPTION A is the answer.