Question:
At a carnival, food tickets cost $2 each and ride tickets cost $3 each. A total of $1,240 was collected at the carnival. The number of food tickets sold was 10 less than twice the number of ride tickets sold.
How many of each type of ticket were sold?
Answer:
350 food tickets and 180 ride tickets were sold
Solution:
Let "x" be the number of food tickets sold
Let "y" be the number of ride tickets sold
Cost of 1 food ticket = $ 2
Cost of 1 ride ticket = $ 3
The number of food tickets sold was 10 less than twice the number of ride tickets sold
Number of food tickets sold = twice the number of ride tickets sold - 10
x = 2y - 10 -------- eqn 1
A total of $1,240 was collected at the carnival
Therefore, we frame a equation as:
number of food tickets sold x Cost of 1 food ticket + number of ride tickets sold x Cost of 1 ride ticket = 1240
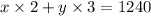
2x + 3y = 1240 ------- eqn 2
Let us solve eqn 1 and eqn 2
Substitute eqn 1 in eqn 2
2(2y - 10) + 3y = 1240
4y - 20 + 3y = 1240
7y = 1260
y = 180
Substitute y = 180 in eqn 1
x = 2(180) - 10
x = 360 - 10
x = 350
Thus 350 food tickets and 180 ride tickets were sold