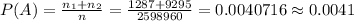Question

Using a 52 card deck, how many 5 card hands have either 5 hearts or 4 hearts and 1 club

Answer 1

10,582

Explanation:

We can choose 5 cards from 52 card deck in

`n = \binom{52}{5} = (52!)/(5!(52-5)!) = (52!)/(5!47!) = \frac{\cancel{47!} \cdot 48 \cdot 49 \cdot 50 \cdot 51 }{5! \cancel{47!}} = ( 48 \cdot 49 \cdot 50 \cdot 51 )/(1 \cdot 2 \cdot 3 \cdot 4 \cdot 5) = 2 \; 598 \; 960`

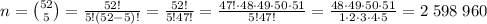
ways.

Now, let's calculate the number of ways we can choose 5 hearts. We know that in a 52 card deck, we have 13 hearts. Therefore, the number of ways to choose 5 hearts is

`n_1 = \binom{13}{5} = (13!)/(5!(13-5)!) = (13!)/(5!8!) = (8! \cdot 9 \cdot 10 \cdot 11 \cdot 12 \cdot 13)/(5!8!) = (9 \cdot 10 \cdot 11 \cdot 12 \cdot 13)/(1 \cdot 2 \cdot 3 \cdot 4 \cdot 5) = 1287`

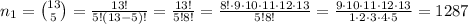
Similarly, number of ways to choose 4 hearts equals
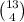`\binom{13}{4}` and number of ways to choose 1 club equals
`\binom{13}{1}`, since there are also 13 clubs in the deck.

Therefore, the number of ways of choosing 4 hearts and 1 club equals

`n_2 = \binom{13}{4} \cdot \binom{13}{1} = 9295`

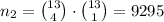
The probability of this event is calculated as

`P(A) = \frac{\text{total number of ways to choose 5 hearts or 4 hearts and a club}}{\text{total number of ways to choose 5 cards from a deck of 52 cards}}`

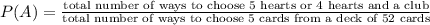
Therefore

`P(A) = (n_1+n_2)/(n) = (1287+9295)/(2598960) =0.0040716 \approx 0.0041`