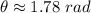Answer:
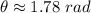
Explanation:
By definition, the Arc lenght can be calculated with the following formula:
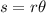
Where "s" is the Arc lenght, "r" is the radius and
 is the central angle measured in radians.
is the central angle measured in radians.
From that equation you can solve for
 dividing both sides of the equation by the radius "r", then:
dividing both sides of the equation by the radius "r", then:
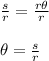
According to the information given in the exercise:
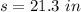
And you can identify in the figure that the radius of the circle is:
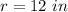
Therefore, you can substitute values into the equation:
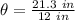
Finally, evaluating, you get the following result:
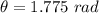
Rounded to the nearest hundredth of a radian: